Chapter 3.2. Simple Conditions – Exam Problems
In the previous chapter, we looked at conditional constructions in the Java language, used to perform various actions depending on a condition. We also mentioned the scope of a variable, as well as how to follow line by line the execution of our program (the so-called debugging). In this chapter, we will practice working with conditional statements, and we'll be looking at some problems given in actual exams. Let's first retrieve some of the newly acquired knowledge on how the conditional statement is constructed:
if (boolean expression) {
// body of the conditional block;
} else {
// body of else-block;
}
if statements consist of:
ifclause- boolean expression - a variable of boolean type (
boolean) or boolean logical expression (an expression that returns a resulttrue / false) - body - contains any block with source code
elseclause and its source code block (optional)
Exam Problems
After recalling how to write conditional statements, let's solve a few problems to get practical experience with the if-else statement.
Problem: Transport Price
A student must travel n kilometers. He has a choice between three modes of transport:
- Taxi. Starting fee: 0.70 BGN. Daily rate: 0.79 BGN/km. Nightly rate: 0.90 BGN/km.
- Bus. Daily/Nightly rate: 0.09 BGN/km. Can be used for distances minimum of 20 km.
- Train. Daily/Nightly rate: 0.06 BGN/km. Can be used for distances at least 100 km
Write a program that enters the number of kilometers n and the period of the day (day or night) and computes the price of the cheapest transport .
Input Data
Two lines are read from the console:
- The first line contains the number n - number of kilometers - integer in the interval [1… 5000].
- The second line contains the word "day" or "night" - if the trip is during the day or at night.
Output Data
Print on the console the lowest price for the specified number of kilometers.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 5 day |
4.65 | 7 night |
7 |
| Input | Output | Input | Output |
|---|---|---|---|
| 25 day |
2.25 | 180 night |
10.8 |
Hints and Guidelines
We will read the input data and depending on the distance we will choose the cheapest transport. For this purpose, we will use several conditional statements.
Input Data
Our first step is to create an object of type java.util.Scanner. We pass in its constructor the "input stream" (System.in) that we are going to read from. In the definition of the problem, we have information about the input and output. The first two lines of the solution will contain the declaration and initialization of the two variables that will store the values of the input data.
The first line is mentioned to contain an integer, so the variable that will be declared is of type int. For the second line, the instruction is that it contains a word, respectively the variable is of type String.

Before we begin with the conditional statements it's necessary to declare one variable that will store the value of the transport price.
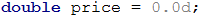
Expression Evaluation and Computing The Relevant Calculations
Once we have declared and initialized the input data and the variable that will store the value of the price, we should assess which conditions of the problem will be the first to be checked.
It is evident from the problem that the rates of two of the vehicles do not depend on whether it is day or night, but the rate of the third transport (taxi) does. This is a reason to pick our first condition to verify whether it's day or night and determine which taxi rate will be in effect. To achieve that we declare another variable that will store the value of the taxi fare.
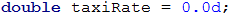
Computing the taxi rate is performed with an if-else statement. That's how we taxi price variable is assigned a value.
Once that's done, we can now proceed to the computation of the full transportation price. Another condition for the price defined in the problem is the traveling distance with a chosen vehicle. Naturally to do that we pick an if-else condition that we used to determine the price for the transport depending on the entered kilometers.

First, we check if the kilometers are below 20 since it's specified in the problem that the student could only use a taxi for destinations that are below 20 kilometers away. If the expression in the first conditional statement is evaluated to be true then the variable that stores the transportation price (price) will be assigned the corresponding value. This value is equal to the initial rate, which we sum up with its rate multiplied by the distance that the student has to travel.
If the expression in the first conditional statement is evaluated to false then the next step of the program is to check if the distance is below 100. The reason we're doing that is to be possible to use a bus as a vehicle in this distance range. The price per kilometer for the bus is lower than the taxi price. Therefore, the result of the expression evaluation is true, then here's the place to assign the value of the transportation price variable (price) which equals the result of the multiplication of the distance and the bus rate.
In the case of the second check not returning true as a result, the program ends up in the else block and assigns a value equal to the result of the multiplication of the distance and the rate of the train. We do that because the train is the cheapest vehicle for the given distance.
Printing The Result
We have successfully computed the price of the cheapest transportation so we're almost at the end of the problem. The only thing left is to print out the result that we have on the console. In our problem, there's no requirement for the resulting output and that's why we choose to keep it simple and just print the variable (price).
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/652#0.
Problem: Pipes In Pool
A Pool with volume V has two filling pipes. Each pipe has a specified hourly flow rate (liters of water that pass through one pipe per hour). The worker opens the pipes at the same time and leaves the sight for N hours. Your problem is to write a program that prints out the state of the pool, at the moment the worker comes back.
Input Data
Four lines are read from the console:
- The first line contains the number V - pool volume in liters - integer in the range [1… 10000].
- The second line contains the number P1 - hourly flow rate of the first tube - integer in the interval [1 … 5000].
- The third line contains the number P2 - hourly flow rate of the second tube - integer in the range [1 … 5000].
- The fourth line contains the number H - number of hours that the employee is absent - a floating-point number in the interval [1.0 … 24.00].
Output Data
Print on the console one of two possible states:
- How full are the pool and each pipe's percentage contribution? Use the whole number before the decimal point of a percentage (i.e. round down).
- "The pool is [x]% full. Pipe 1: [y]%. Pipe 2: [z]%."
- If the pool has overflowed - how many liters over the pool's volume has the pool overflowed for the given time, floating-point number.
- "For [x] hours the pool overflows with [y] liters." \ Have in mind that due to the percentage rounding some data may be lost and it's okay for *the sum of the percentages to be 99% and not 100%.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 1000 100 120 3 |
The pool is 66% full. Pipe 1: 45%. Pipe 2: 54%. | 100 100 100 2.5 |
For 2.5 hours the pool overflows with 400 liters. |
Hints and Guidelines
To solve the problem we'll read from the standard input stream, utilize several conditional statements and computations, and print our result to the console.
Input Data
By definition, our program has to have four lines that are going to read and store the input data. The first three are going to store whole numbers and this is a reason we pick the int type for those variables. On the fourth line, we are supposed to get a floating-point number and that's why the variable that we're going to use is of type double.

Our next step is to declare and initialize a variable that will store the computed value for the amount of water that the pool has filled up with while the worker has been away. The calculation is made by summing up the flow rate of the two pipes and multiplying them by the input hours H.

Expression Evaluation and Computing The Relevant Calculations
Once we have the amount of water that has passed through the pipes, the next step is to compare it with the volume of the pool.
We will do this with a simple if-else conditional statement, in which the condition will be whether the amount of water is less than the volume of the pool. If the check returns true, then we need to print a line that contains the ratio between the amount of water that has passed through the pipes and the volume of pool, as well as the ratio of the amount of water from each pipe to the pool volume**.
The ratio needs to be expressed in percentage that's why we'll multiply by 100 the result of all the prior calculations on this line. The values will be interpolated using formatting strings and rounded down to integer with Math.floor (…) (it's a requirement of the problem).
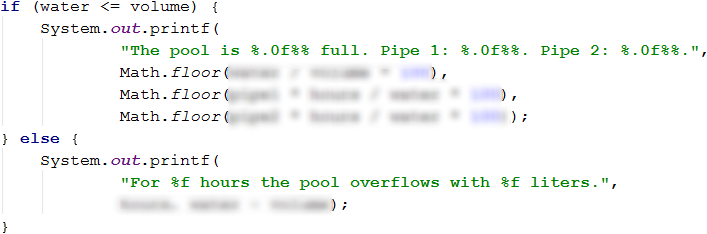
However, if the check returns false it means that the amount of water is greater than the volume of the pool, respectively it has overflowed. Again, the output must be one line but this time it should contain only two values - away time in hours of the worker and the amount of overflowed water.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/652#1.
Problem: Sleepy Cat Tom
The cat Tom enjoys sleeping all day, unfortunately whenever his owner has some free time he comes to play with Tom. To have a good sleeping routine Tom's norm for playtime is 30 000 minutes per year*. Tom's playtime is dependent on his owner's non-working days:
- When Tom's owner is at work, Tom's playtime is 63 minutes a day.
- When Tom's owner has a day off, Tom's playtime is 127 minutes a day.
Your problem is to write a program that takes as input Tom's owner's number of days off and prints out whether Tom has a satisfactory sleeping routine and how much is the difference from Tom's norm for playtime for the current year, assuming that the year has 365 days.
Example: 20 days off → 345 working days (365 - 20 = 345). The actual playing time is 24 275 minutes (345 \ 63 + 20 \ 127). The difference from the norm is 5 725 minutes (30 000 - 24 275 = 5 725) or 95 hours and 25 minutes.
Input Data
The input data is read from the console and consists of an integer - Tom's owner number of days off, number in the range [0 … 365].
Output Data
Two lines are to be printed on the console.
- If Tom's playing time is above the norm for the current year:
- On the first line print: "Tom will run away".
- On the second line print the difference from the norm in the format: "{H} hours and {M} minutes more for play".
- If Tom's playing time is below the norm for the current year:
- On the first line print: "Tom sleeps well".
- On the second line print the difference from the norm in the format: "{H} hours and {M} minutes less for play".
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 20 | Tom sleeps well 95 hours and 25 minutes less for play |
113 | Tom will run away 3 hours and 47 minutes more for play |
Hints and Guidelines
To solve the problem we'll read from the standard input stream, utilize several conditional statements and computations, and print our result to the console.
Input Data
The input data will be read in a single line that will contain a whole number in the range [0 … 365]. That's why the variable that'll store the value is going to be of type int.

Our first step is to calculate how many minutes in total has Tom and his master played together. The problem states that not only has the sleepy cat played on days off but also on working days. The number that we read from the console is the number of non-working days.
Our next step is to use that number to calculate how many are the working days of Tom's owner. We need this number because without it we can not get the total number of playtime minutes. The total number of days in a year is 365, the number of days off is X, which means that the number of working days is 365 - X. We will store the difference in a new variable (workingDays), which we will use only for this value.
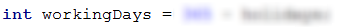
Now that we have the number of days to play, we can now calculate Tom's playing time in minutes. Its value is equal to the result of the multiplication of the working days by 63 minutes (in the problem it's specified that on working days the playing time is 63 minutes per day) added to the result of the multiplication of days off and 127 minutes (in the problem it's specified that on days off the playing time is 127 minutes per day).

We need to print the difference between hours and minutes. That's why we'll subtract from the total playing time Tom's playtime norm of 30 000 minutes and we'll store the result in a new variable. After that, we'll use that new variable to divide without a remainder to 60 and that's how we'll get the hours. To get the number of minutes we'll utilize the modulo operator % and get the remainder of the division by 60.
Note that if Tom's resulting playtime is less than 30 000 when we subtract the norm we'll get a negative number. We can fix that with the method Math.abs(…) when subtracting.

Conditional Expressions Verification
The playing time is already calculated which leads us to the next step - Tom's playtime and Tom's norm comparison. We'll use an if-else conditional statement. It'll verify in its if clause whether the playtime is larger than 30 000 (norm).
Output Data Processing
Depending on the result of the evaluation of the boolean expression our objective is to print the difference in hours and minutes. We'll do that using the formatting specifier and the previously computed hour and minutes values. The given output examples show that the printed values are formatted as a rounded down whole number. This is a cue that we should be using Math.floor(…) when we're printing the result.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/652#2.
Problem: Harvest
There's a vineyard that has an area of X sq. M.. 40% of the harvest is allocated for wine production. The yield from 1sq.m. vineyard is Y kilograms of grapes. To produce 1 liter of wine is used 2.5kg grapes. The desired amount of wine for sale is Z liters.
Your problem is to write a program that calculates the possible amount of produced wine and validates if it's enough. If the production is satisfying the expectations, then the remainder shall be distributed equally among the vineyard workers.
Input Data
Four lines are read from the console:
- The first line contains the area of the vineyard X sq.m - integer in the interval [10 … 5000].
- The second line contains the grapes yield per square meter Y - a real number in the interval [0.00 … 10.00].
- The third line contains the desired amount of wine Z liters - an integer in the range [1 … 600].
- The fourth line contains the number of workers - integer in the interval [1 … 20].
Output Data
The following is expected to be printed on the console:
- If the produced wine is less than the required:
- "It will be a tough winter! More {insufficient wine} liters wine needed."
- The result should be rounded down.
- "It will be a tough winter! More {insufficient wine} liters wine needed."
- If the produced wine is sufficient:
- "Good harvest this year! Total wine: {total wine} liters."
- The result must be rounded down.
- "{Wine left} liters left -> {wine for 1 worker} liters per person."
- Both results must be rounded up.
- "Good harvest this year! Total wine: {total wine} liters."
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 650 2 175 3 |
Good harvest this year! Total wine: 208 liters. 33 liters left → 11 liters per person. |
1020 1.5 425 4 |
It will be a tough winter! More 180 liters of wine are needed. |
Hints and Guidelines
To solve the problem we'll read from the standard input stream, utilize several conditional statements and computations, and print our result to the console.
Input Data
First, we need to check what input data is expected and choose an adequate type for each of the variables that will store this data.

To solve the problem we need to compute the amount of wine in liters that the harvest will produce using the input data. The problem defines a formula that requires the weight of the yielded grapes in kg.. We can easily calculate this by declaring a variable that will store a value equal to 40% of the result of the multiplication of the area of the vineyard and the amount of yielded grapes per square meter.
Once we have made these calculations, we are ready to insert them into the problem formulation. We declare another variable that will store the amount of wine in liters and will be equal to the weight of the yielded grapes in kg. divided by 2.5.

Expression Evaluation and Processing The Output Data
Our next step is to check if the produced wine is enough. We'll use a simple if-else conditional statement with a clause that verifies if the amount of wine in liters produced from the harvest is more than or equal to the desired liters.
If the expression evaluation returns true, then on the first line we should print the amount of wine produced by these harvesters. It's required that this value should be rounded down. To comply with the requirement we'll use the method Math.floor(…) when printing it using the formatting specifier.
The requirement for the second line is to print the interpolated values rounded up. We'll use the method Math.ceil(…). The values that we have to print are the wine that's left and the amount of wine that is to be given to each worker. The wine that's left is equal to the difference between the produced liters of wine and the desired liters of wine. As the result of this computation, we'll store in a new variable that we'll declare and initialize in the body block of the if statement before printing the first line. The amount of wine that is to be given to each worker we'll get by dividing the difference by the number of workers.
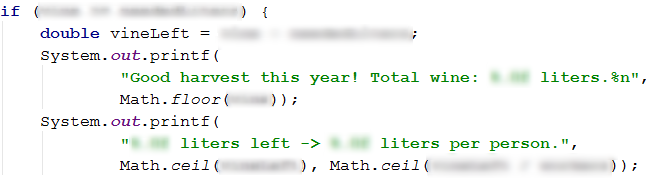
If the expression evaluation returns false, then we need to print the difference between desired liters of wine and the produced liters of wine from this harvest. It's required that this value should be rounded down. To comply with the requirement we'll use the method Math.floor(…) when printing it using the formatting specifier.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/652#3.
Problem: Firm
A company is requested to develop a project that is estimated for a given number of hours. The company has a certain number of days to do that. In 10% of those days, its employees are being onboarded and are not ready to work on the project. A normal working day at this company lasts for 8 hours. The project is important for the company and every employee is obliged to work on this project overtime for 2 hours per day.
The hours should be rounded down (e.g. 6.98 hours are rounded to 6 hours).
Your problem is to write a program that calculates if the company is going to finish the project on time and how many hours more are needed for the completion of the project or if the execution was successful how many dedicated working hours are left at hand.
Input Data
Three lines are read from the console:
- The first line contains the necessary number of working hours - an integer in the interval [10 … 200 000].
- The second line contains the days that the company has to finish the project - an integer in the interval [0 … 20 000].
- The third line contains the number of all employees - an integer in the range [1 … 600].
Output Data
One line is expected to be printed on the console:
- If the time is enough:
- "Yes! {hours left} hours left.
- If the time is NOT enough:
- "Not enough time! {hours needed} hours needed.".
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 90 7 3 |
Yes!99 hours left. | 99 3 1 |
Not enough time!72 hours needed. |
Hints and Guidelines
To solve the problem we'll read from the standard input stream, utilize several conditional statements and computations, and print our result to the console.
Input Data
First, we need to check what input data is expected and choose an adequate type for each of the variables that will store this data.

Auxiliary Calculations
The next step is to calculate the number of working hours. This we can do by multiplying the working days by 8 (every working day is 8 hours) and the number of the company's employees. On top of that, we should add the overtime too. The working days are equal to 90% of the days that the company has. The overtime is equal to the result of the multiplication of the employees and 2 (decided overtime length) and the number of days that the company has. We can see that the problem requires the working hours to be rounded down. That's something we can easily do by using the method Math.floor(…).

Performing Verifications
Once we've made the calculations we need to compute the value of the working hours we should check whether these hours are enough.
If the time is enough we print the difference between the working hours and the estimated hours for the project.
If the time is not enough we print the additional hours that are needed to finish the project. And that is the difference between the estimated hours and the working hours.
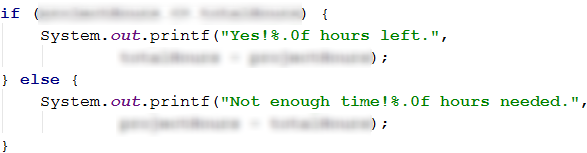
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/652#4.