Chapter 7.1. More Complex Loops
Having learned what for loops are and what they serve for, it is now time to get to know other types of loops and some more complex loops constructs. They will expand our knowledge and help us solve more challenging problems. In particular, we will have a look at how the following constructs are used:
- loops with a step
whileloopsdo-whileloops- infinite loops
In the current, chapter we will also get acquainted with the break statement and how to terminate a loop using it. We will also learn how to keep track of errors during the execution of our program, using a try-catch block.
Video
Loops With a Step
In chapter "Loops", we learned how the for loop works, and we already know when and for what purpose to use it. In this topic, we will pay attention to a specific and very important part of its construction, namely the step.
What is a Step?
The step is that part of the for loop construction that states how much to increase or decrease the value of its leading variable. It is declared last in the for loop block.
It most often has a size 1 and in that case instead of writing i += 1 or i -= 1, we can use the i++ or i-- operators. If we want the step to be different than 1, we use the operator i += (step size) to increment and i -= (step size) to decrement. For a step size of 10, the loop would look like this:
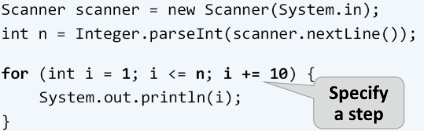
The following is a series of examples, the solution of which will help us better understand the use of the step in the for loop.
Problem: Numbers 1...N with Step 3
Write a program that prints the numbers from 1 to n with a step 3. For example, if n = 100, the result will be 1, 4, 7, 10, …, 94, 97, 100.
We can solve the problem through the following sequence of actions (algorithm):
- We read the number
nfrom the console input. - We run a
forloop from 1 tonwith a step size of 3. - We print the value of the current step in the body of the loop.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#0.
Problem: Numbers N...1
Write a program that prints the numbers from n to 1 in reverse order (step -1). For example, if n = 100, the result will be 100, 99, 98, …, 3, 2, 1.
We can solve the problem in the following way:
- We read the number
nfrom the console input. - We run a
forloop in which we assignint i = n. - We reverse the loop condition:
i >= 1. - We define the step size as -1.
- We print the value of the current step in the body of the loop.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#1.
Problem: Powers of Two
In the following example, we will have a look at using the usual step with size 1 but with a slightly different logic in the body of the loop.
Write a program that prints the numbers from 1 to 2^n (two to the power of n). For example, if n = 10, the result will be 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#2.
Problem: Even Powers of 2
Print the even powers of 2 to 2^n: 2^0, 2^2, 2^4, 2^8, …, 2^n. For example, if n = 10, the result will be 1, 4, 16, 64, 256, 1024.
Here is a way to solve the problem:
- We create a variable
numfor the current number to which we assign an initial value of 1. - We set a value of 2 for the step of the loop.
- In the body of the loop, we print the value of the current step and increase the current number
num4 times (as per the condition of the problem).

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#3.
While Loop
The next type of loops we will get acquainted with are called 'while' loops. What is specific about them is that they repeat a block of commands, as long as a given condition is true. Their structure differs from the for loops, and they even have a simplified syntax.
What is a While Loop?
In programming, the while loop is used when we want to repeat the execution of a certain logic while a given condition is met. We define 'condition' as any expression that returns 'true' or 'false'. When the condition is false, the while loop terminates and the program continues with the execution of the code following the loop. The while loop construction looks like this:
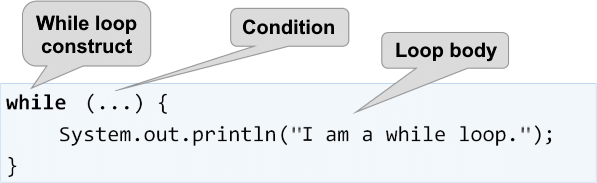
The following is a series of examples, the solution of which will help us better understand the use of the while loop.
Problem: Sequence 2k+1
Write a program that prints all numbers ≤ n from the sequence: 1, 3, 7, 15, 31, …, having in mind that each next number = previous number * 2 + 1.
Here is how we can solve the problem:
- We create a variable
numfor the current number to which we assign an initial value of 1. - We put the current number <= n as the loop condition.
- In the body of the loop, we print the value of the current number and increase the current number, using the formula from the problem.
Here is a sample representation of the described steps:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#4.
Problem: Numbers in Range [1…100]
Enter an integer in the range [1 … 100]. If it is invalid, input an integer again. In this case, we will consider any number that is not in the specified range as invalid.
We can solve the problem through the following algorithm:
- We create a variable
num, to which we assign the integer value obtained from the console input. - For a loop condition, we put an expression, that is
trueif the number of the input is not in the range specified in the problem condition. - In the body of the loop: we print a message "Invalid number!" on the console, and then we assign a new value to
numfrom the console input. - Having validated the input number, we print its value outside the body of the loop.
Here is a sample representation of the algorithm, using a while loop:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#5.
Greatest Common Divisor (GCD)
Before proceeding to the next problem, it is necessary to get acquainted with the definition of the greatest common divisor (GCD).
Definition of GCD: the greatest common divisor of two natural numbers a and b is the largest number that divides simultaneously both a and b without a remainder. For example:
| a | b | GCD |
|---|---|---|
| 24 | 16 | 8 |
| 67 | 18 | 1 |
| 12 | 24 | 12 |
| 15 | 9 | 3 |
| 10 | 10 | 10 |
| 100 | 88 | 4 |
The Euclidean Algorithm
In the next problem, we will use the Euclidean algorithm, one of the first published algorithms for finding the GCD:
Until we reach a remainder of 0:
- We divide the larger number by the smaller one.
- We take the remainder of the division.
Pseudocode for the Euclidean algorithm:
while b ≠ 0
var oldB = b;
b = a % b;
a = oldB;
print a;
Problem: Greatest Common Divisor (GCD)
Enter integers a and b and find GCD(a, b).
We will solve the problem using the Euclidean algorithm:
- We create
aandbvariables, to which we assign the integer values obtained from the console input. - For a loop condition, we put an expression that is
trueif thebnumber is different than 0. - In the body of the loop: we follow the conditions of the pseudocode:
- We create a temporary variable, to which we assign the current value of
b. - We assign a new value to
b, which is the remainder of the division ofaandb. - We assign the previous value of the
bvariable toa.
- We create a temporary variable, to which we assign the current value of
- Once the loop is complete and, we have found the GCD, we print it on the screen.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#6.
Do-While Loop
The next type of loop we will get acquainted with is the do-while. It resembles the while loop by structure, but there is a significant difference between the two. It consists in the fact that do-while will execute its body at least once. Why is this happening? At do-while loop construction, the condition is always checked after its body, which ensures that the code will be executed after the first loop iteration, and the check for the loop termination will be applied to each subsequent iteration of the do-while.

The following is the usual series of sample problems, the solution of which will help us better understand the use of the do-while loop.
Problem: Factorial
Calculate n! = 1 * 2 * 3 * … * n, where n is a natural number. For example, if n = 5, the result will be: 5! = 1 * 2 * 3 * 4 * 5 = 120.
Here is how we can calculate the factorial:
- We create the variable
n, to which we assign the integer value obtained from the console input. - We create another variable -
fact, with the initial value of 1. We will use it to calculate and store the factorial. - For a loop condition, we will use
n > 1, since each time we perform the calculations in the body of the loop, we will reduce the value ofnby 1. - In the body of the loop:
- We assign a new value to the
fact, which is the result of multiplying the current values offactandn. - We decrease the value of
nby -1.
- We assign a new value to the
- We print the final value of the factorial outside the body of the loop.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#7.
Problem: Sum Digits
Sum the digits of a positive integer n. For example, if n = 5634, the result will be: 5 + 6 + 3 + 4 = 18.
We can use the following idea to solve the problem:
- We create the variable
nto which we assign a value equal to the number entered by the user. - We create a second variable -
sum, with the initial value of 0. We will use it to calculate and store the result. - For a loop condition, we will use
n > 0, since we will remove the last digit ofnafter each calculation of the result in the body of the loop. - In the body of the loop:
- We assign a new value to
sum, equals to the sum of the current value ofsumand the last digit ofn. - We assign a new value to
n, which is the result of removing the last digit ofn.
- We assign a new value to
- We print the final value of the sum outside the body of the loop.

n % 10: returns the last digit of the number n.n / 10: deletes the last digit of n. |
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#8.
Infinite Loops and break Operator
So far, we got acquainted with different types of loops and learned about their constructions and how they are applied. Now, we need to understand what an infinite loop is, when it occurs and how we can terminate its execution through the break operator.
What is an Infinite Loop?
An infinite loop repeats infinitely the execution of its body. For while and do-while loops the check for the end of a loop is a conditional expression that always returns true. An infinite for occurs when there is no condition to end the loop.
Here is what an infinite while loop looks like:

And here is what an infinite for loop looks like:

The break Operator
We already know that the infinite loop executes a specific code to infinity, but what if we want to forcibly exit the loop under a given condition at some point? In this situation, the break operator comes in handy.
The break operator stops the loop execution at the moment it is called and continues from the first line after the end of the loop. This means that the current iteration of the loop will not be completed and, accordingly the rest of the code in the body of the loop will not be executed. |
Problem: Prime Number Checking
The next problem we are going to solve requires conducting a prime number check. Before proceeding with it, let’s remember what prime numbers are.
Definition: an integer is prime when it is divisible without remainder only to itself and 1. By definition, prime numbers are positive and greater than 1. The smallest prime number is 2.
We can assume that an integer n is prime if n > 1 and n is not divisible by any of the numbers between 2 and n-1.
The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, …
In contrast, non-prime (composite) numbers are such numbers that are composed of the product of prime numbers.
Here are a few examples of composite numbers:
- 10 = 2 * 5
- 42 = 2 3 7
- 143 = 13 * 11
Verification algorithm whether an integer is prime: we check if n > 1 and n are divisible by 2, 3, …, n-1 without remainder.
- If it is divisible by any of the numbers, it is composite.
- If it is not divisible by any of the numbers, then it is prime.
We can optimize the algorithm by checking the divisors to √n instead of n-1. Think about the reason why. |
Problem: Check Prime
Check if a number n is prime. To do so, we will check if n is divisible by the numbers between 2 and √n.
Here is the algorithm for prime number verification, described in steps:
- We create the variable
n, to which we assign the integer value obtained from the console input. - We create a boolean variable -
isPrimewith an initial valuetrueif the number is equal or greater than two (since by definition, numbers such as 0, 1, -1, and -2 are non-prime). We assume that a number is prime until proven otherwise. - We create a
forloop, and we assign 2 as an initial value of the loop variable and its current value<= √nas a condition. The step of the loop is 1. - In the body of the loop, we check if
ndivided by the current value has a remainder. If there is no remainder, we change the value ofisPrimetofalseand forcibly terminate the loop with abreakoperator. - Depending on the
isPrimevalue, we print whether the number is prime (true) or composite (false).
Here is a sample implementation of the described algorithm:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#9.
Problem: Enter Even Number
Write a program that checks if a number n is even – if it is, prints it on the screen. An even number is each number that is divisible by 2 without a remainder. In the case of an invalid number, it should be re-input, and a message stating that the number is not even should be displayed.
Here is an idea of how to solve the problem:
- We create a variable
n, to which we assign an initial value of 0. - We create an infinite
whileloop and puttrueas a condition. - In the body of the loop:
- We take the integer obtained by the console input and assign it to
n. - If the number is even, we exit the loop with a
break. - Otherwise, we display a message stating that the number is not even. The iterations continue until an even number is entered.
- We take the integer obtained by the console input and assign it to
- We print the even number on the screen.
Here is a sample implementation of the idea:

Note: although the code above is correct, it will not work if the user enters text instead of numbers, for example, Invalid number. Then the parsing of the input text to a number will break, and the program will display an error message (exception). Later in this chapter, we will learn how to deal with this problem and how to catch and handle exceptions using the try-catch construct.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#10.
Nested Loops and The break Operator
Having learned what nested loops are and how the break operator performs, it is time to understand how they both work together. For a better understanding, let’s write a step-by-step program that should make all possible combinations of pairs of numbers. The first number of the combination is increasing from 1 to 3, and the second one is decreasing from 3 to 1. The problem must continue running until i + j is not equal to 2 (i.e., i = 1 and j = 1).
The desired result is:

Here is one wrong solution, which seems correct at first glance:

If we leave our program this way, the result will be the following:
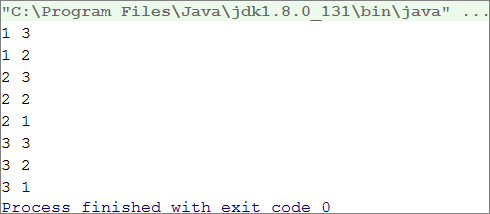
Why does this happen? As we can see, the result is missing 1 1. When the program reaches the point that i 1 and j 1, it enters the if check and performs the break operation. Thus, we exit the inner loop, but then the execution of the outer loop continues. i increases, the program enters the inner loop and prints the result.
When we use the break operator in a nested loop, it interrupts the execution of the inner loop only. |
What is the correct solution? One way of solving this problem is by declaring a bool variable, which keeps track of whether the loop should continue. In case of need to exit (from all nested loops), the variable is set to 'true' and exits the internal cycle with a 'break', and at the next check, will exit from the outer loop. Here is a sample implementation of this idea:
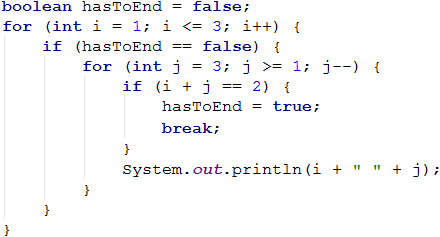
Thus, when i + j = 2, the program will set the hasToEnd = true and exit the inner loop. Upon the next iteration of the outer loop due to the if check, the program will not reach the inner loop and interrupt its execution.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#11.
Error Handling: try-catch Construction
The last thing we will get familiar with within this chapter is how to "catch" errors with the try-catch construction.
What is a try-catch?
The try-catch program construction is used to intercept and handle exceptions (errors) during the program execution.
In programming, exceptions are notifications of an event that disrupts the normal operation of a program. Such exceptional events interrupt the execution of our program, and it is looking for something to handle the situation. If it does not find it, the exception is printed on the console (the program "fails"). If it finds, the exception is processed and the program continues its normal execution without "failing". In a bit, we will see how this happens.
When an exception occurs, the exception is said to have been ”thrown” (throw exception). Hence the expression ”catch exception”.
The try-catch Construction
The try-catch construction has different types, but for now, we will get acquainted only with the most basic of them, where the catch block will intercept any error in a variable named ex

In the next problem, we will see how to handle a situation where the user enters an input other than a number (for example, string instead of int) using try-catch .
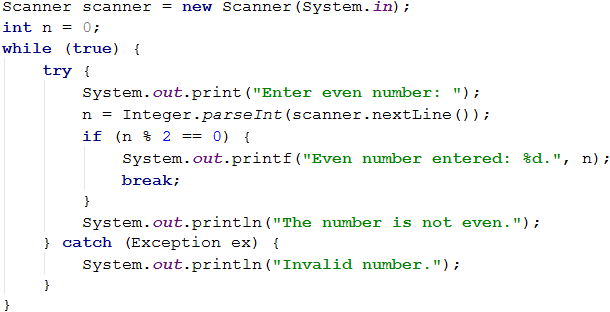
Problem: Enter Even Number (with Text Input)
Write a program that checks if a number n is even – if it is, prints it on the screen. Upon entering an invalid number, a message appears stating that the input data is not a valid number, and another input data must be made.
Here is how we can solve the problem:
- We create an infinite
whileloop, for which we settrueas a condition. - In the body of the loop:
- We create a
try-catchconstruction. - In the
tryblock, we write the programming logic for reading the user input, parsing it to a number, and then checking for an even number. - If the number is even, we print it and exit the loop (with
break). The program is done, and it ends. - If the number is odd, we print a message that an even number is required, without exiting the loop (since we want to repeat the step by entering input data).
- If we catch an exception upon executing the
tryblock, we write a message for an invalid input number, and the loop is repeated because we do not explicitly exit it.
- We create a
Here is a sample implementation of the described idea:
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#12.
Now the solution should always work whether we enter integers, invalid numbers (for example, too many digits), or texts that do not contain numbers.
Problems with Loops
In this chapter, we have introduced several new types of loops that we can use to make repetitions with more complex program logic. Let's solve several problems using the new knowledge.
Problem: Fibonacci
In mathematics, Fibonacci numbers form a series that looks like this: 1, 1, 2, 3, 5, 8, 13, 21, 34, …
The formula to form the sequence is:
F0 = 1
F1 = 1
Fn = Fn-1 + Fn-2
Sample Input and Output
| Input (n) | Output | Comment |
|---|---|---|
| 10 | 89 | F(11) = F(9) + F(8) |
| 5 | 8 | F(5) = F(4) + F(3) |
| 20 | 10946 | F(20) = F(19) + F(18) |
| 0 | 1 | |
| 1 | 1 |
Write a program in which we enter an integer number n and calculate the n-number of Fibonacci.
Hints and Guidelines
An idea to solve the problem:
- We create a
nvariable, to which we assign the integer value obtained from the console input. - We create
f0andf1variables to which we assign value 1 since this is how the sequence begins. - We create a
forloop with a condition current valuei < n - 1. - In the body of the loop:
- We create a temporary variable
fNextto which we assign the next number of the Fibonacci sequence. - We assign the current value of
f1tof0. - We assign the value of the temporary variable
fNexttof1.
- We create a temporary variable
- We print the n-number of Fibonacci outside the loop.
Sample implementation:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#13.
Problem: Number Pyramid
Print the numbers 1… n in a pyramid as in the examples below. On the first line, we print one number on the second line, we print two numbers, on the third line, we print three numbers, etc., until the numbers run out. On the last line, we print as many numbers as we have left until we get to n.
Sample Input and Output
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 7 | 1 2 3 4 5 6 7 |
5 | 1 2 3 4 5 |
10 | 1 2 3 4 5 6 7 8 9 10 |
Hints and Guidelines
We can solve the problem with two nested loops (by rows and columns) by printing in them and leaving when reaching the last number. Here is the idea, described in more detail:
- We create a
nvariable, to which we assign the integer value obtained from the console input. - We create a
numvariable with an initial value of 1. It will keep the number of printed numbers. At each iteration, we will increase it by 1 and print it. - We create an outer
forloop, which will be responsible for the rows in the table. We name the loop variable as arowand assign it an initial value of 0. We setrow < nas a condition. The size of the step is 1. - In the body of the loop, we create an inner
forloop, which will be responsible for the columns in the table. We name the loop variable ascoland assign it an initial value of 0. We setcol < row(row= number of digits per line) as a condition. The size of the step is 1. - In the body of the loop:
- We check if
col > 1and if yes – we print space. If we don't perform this check and directly print space, we will have an unnecessary one at the beginning of each line. - We print the number
numin the current cell of the table and increase it by 1. - We perform a check for
num > n. Ifnumis greater thann, we break the inner loop.
- We check if
- We print a blank line to proceed to the next one.
- We check again if
num > n. If it's greater, we interrupt the execution of our program with abreak.
Here is a sample implementation:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#14.
Problem: Number Table
Print the numbers 1 … n in a table as per the examples below.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 3 | 1 2 3 2 3 2 3 2 1 |
4 | 1 2 3 4 2 3 4 3 3 4 3 2 4 3 2 1 |
Hints and Guidelines
We can solve the problem with two nested loops and a few calculations inside:
- We read from the console the table size in an integer variable
n. - We create a
forloop, which is responsible for the table rows. We name the loop variable as arowand assign it an initial value 0. We setrow < nas a condition. The size of the step is 1. - In the body of the loop, we create a nested
forloop, which is responsible for the table columns. We name the loop variable ascoland assign it an initial value of 0. We setcol < nas a condition. The size of the step is 1. - In the body of the nested loop:
- We create a
numvariable, to which we assign the result of current row + current column + 1 (+1, since we start counting from 0). - We perform a check if
num > n. Ifnumis greater than n, we assign a new value of two times n - current value ofnumtonum. We do this to not exceednin any of the table cells.- We print the number from the current table cell.
- We create a
- We print a blank line in the outer loop to proceed to the next one.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/659#15.
What Have We Learned from This Chapter?
We can use the for loops with a step:
for (int i = 1; i <= n; i+=3) {
System.out.println(i);
}
The while / do-while loops are repeated as long as a given condition is true:
int num = 1;
while (num <= n) {
System.out.println(num++);
}
If we need to interrupt the loop execution, we use the break operator:
int n = 0;
while (true) {
n = Integer.parseInt(scanner.nextLine());
if (n % 2 == 0) {
break; // even number -> exit from the loop
}
System.out.println("The number is not even.");
}
System.out.println("Even number entered: {0}", n);
We already know how to catch errors during the execution of our program:
try {
System.out.println("Enter even number: ");
int n = Integer.parseInt(scanner.nextLine());
} catch (Exception ex) {
System.out.println("Invalid number.");
}
// If Integer.parseInt(…) fails, the catch { … } block will be executed