Chapter 9.1. Problems for Champions – Part I
In this chapter, we will offer the reader more complex problems. They aim to develop algorithmic skills and acquire programming techniques to solve problems with higher complexity.
More Complex Problems on The Studied Material
We will solve several programming problems that cover the material studied in the book but are more difficult than the usual problems of the practical exams at SoftUni. If you want to become a champion of the basics of programming, we recommend this training to solve such complex problems to make it easy for you to take exams.
Problem: Crossing Sequences
We have two sequences:
- a sequence of Tribonacci (by analogy with the Fibonacci sequence), where each number is the sum of the previous three (with given three numbers)
- a sequence generated by a numerical spiral defined by looping like a spiral (right, bottom, left, top, right, bottom, left, top, etc.) of a matrix of numbers starting from its center with a given starting number and incremental step, by storing the current numbers in the sequence each time we make a turn
Write a program that finds the first number that appears in both sequences defined as described above.
Problem
Let the Tribonacci sequence start with 1, 2 and 3. This means that the first sequence will contain the numbers 1, 2, 3, 6, 11, 20, 37, 68, 125, 230, 423, 778, 1431, 2632, 4841, 8904, 16377, 30122, 55403, 101902, and so on.
At the same time, let the numbers in the spiral begin with 5, and the spiral increases by 2 at each step.
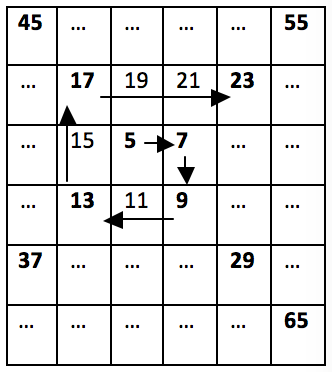
Then the second sequence will contain the numbers 5, 7, 9, 13, 17, 23, 29, 37, and so on. We see that 37 is the first number to be found inside the Tribonacci sequence and the spiral one, and that is the desired solution to the problem.
Input Data
Input data should be read from the console.
- On the first three lines of the input we will read three integers, representing the first three numbers in the Tribonacci sequence, positive non-zero numbers, sorted in ascending order.
- On the following two lines of the input, we will read two integers representing the first number and the step for each matrix's cell for the spiral of numbers. The numbers representing the spiral are positive non-zero numbers.
Input data will always be valid and will always be in the format described. There is no need to check.
Output Data
The result should be printed on the console.
On the single line of the output, we must print the smallest number that occurs in both sequences. If there is no number in the range [1 … 1 000 000], which can be found in both sequences, print "No".
Constraints
- All numbers in the input will be in the range [1 … 1 000 000].
- Allowed program time: 0.3 seconds.
- Allowed memory: 16 MB.
Sample Input and Output
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 1 2 3 5 2 |
37 | 13 25 99 5 2 |
13 | 99 99 99 2 2 |
No |
| Input | Output | Input | Output |
|---|---|---|---|
| 1 1 1 1 1 |
1 | 1 4 7 23 3 |
23 |
Hints and Guidelines
The problem seems quite complicated, so we will break it into simpler sub-problems.
Processing The Input Data
The first step in solving the problem is to read and process the input. Input data consists of 5 integers: 3 for the Tribonacci sequence and 2 for the numerical spiral.

Once we have the input data, we need to think about how we will generate the numbers in the two sequences.
Generating Tribonacci Sequence
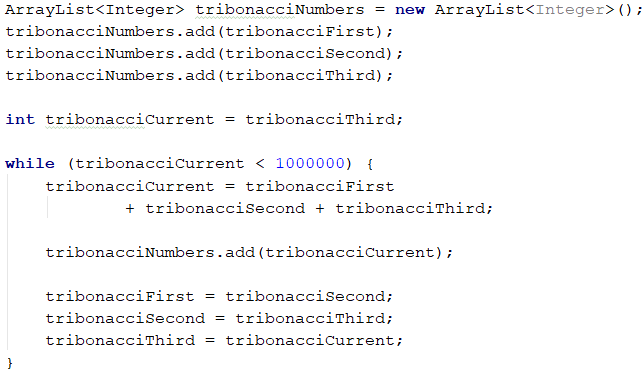
For the Tribonacci sequence, we will always sum up the previous three values and then move the values of those numbers (the three previous ones) to one position in the sequence, i.e., the value of the first one must accept the value of the second one, and so on. When we are ready with the number, we will store its value in an array. Since the problem description states that the numbers in the sequences do not exceed 1,000,000, we can stop generating this range at 1,000,000.
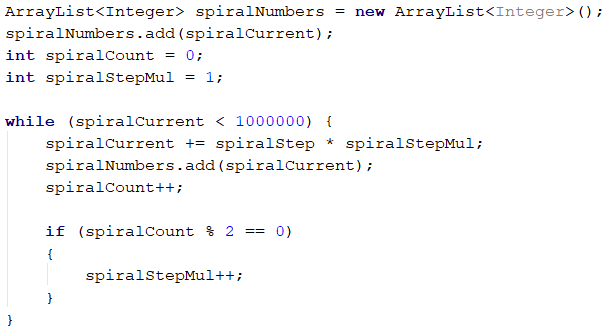
Generating Numerical Spiral
We need to think of a relationship between numbers in the numerical spiral so we can easily generate every next number without having to look at matrices and loop through them. If we carefully look at the picture from the description, we will notice that every 2 "turns" in the spiral, the numbers we skip are increased by 1, i.e. from 5 to 7 and from 7 to 9, not a single number is skipped, but we directly add with the step of the sequence. From 9 to 13 and from 13 to 17 we skip a number, i.e. we add the step twice. From 17 to 23 and from 23 to 29 we skip two numbers, i.e. we add the step three times and so on.
Thus, we see that for the first two we have the last number + 1 * the step, the next two we add with the 2 * the step, and so on.
Every time we want to get to the next number of the spiral, we will have to make such calculations.
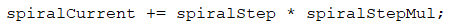
What we have to take care of is for every two numbers, our multiplier (let's call it "coefficient") must increase by 1 (spiralStepMul++), which can be achieved with a simple check (spiralCount % 2 == 0). The whole code from the generation of the spiral in an array is given below.
Finding Common Number for The Sequences
Once we have generated the numbers in both sequences, we can combine them and build the final solution. How will it look? For each of the numbers in the first sequence (starting from the smaller one), we will check if it exists in the other one. The first number that meets this criterion will be the answer to the problem.
We will do a linear search in the second array. We will leave, the more curious readers, to optimize it using the technique called binary search because the second array is generated in sorted form, i.e., it meets the requirement to apply this type of search. The code for finding our solution will look like this:
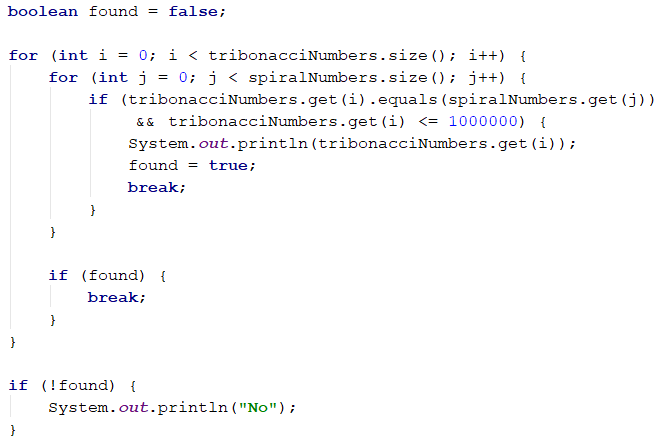
The previous solution to the problem uses arrays to store the values. Arrays are not needed to solve the problem. There is an alternative solution that generates the numbers and works directly with them instead of keeping them in an array. On every step, we can check whether the numbers in the two sequences match. If this is the case, we will print the number on the console and terminate the execution of our program. Otherwise, we will see the current number of which sequence is the smaller one, and we will generate the next one where we are "lagging". The idea is that we will generate numbers from the sequence that is "behind" until we skip the current number of the other sequence and then vice versa, and if we find a match in the meantime, we will terminate the execution.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/663#0.
Problem: Magic Dates
Date is given in a "dd-mm-yyyy" format, e.g. 17-04-2018. We calculate the weight of that date by taking all of its digits, multiplying each digit with the others after it, and finally summing up all the results obtained. In our case, we have 8 digits: 17032007, so the weight is 1*7 + 1*0 + 1*3 + 1*2 + 1*0 + 1*0 + 1*7 + 7*0 + 7*3 + 7*2 + 7*0 + 7*0 + 7*7 + 0*3 + 0*2 + 0*0 + 0*0 + 0*7 + 3*2 + 3*0 + 3*0 + 3*7 + 2*0 + 2*0 + 2*7 + 0*0 + 0*7 + 0*7 = 144.
Our problem is to write a program that finds all the magical dates between two specific years (inclusively) corresponding to the given weight. Dates must be printed in ascending order (by date) in the format "dd-mm-yyyy". We will only use the valid dates in the traditional calendar (the leap years have 29 days in February).
Input Data
Input data should be read from the console. It consists of 3 lines:
- The first line contains an integer: start year.
- The second line contains an integer: end year.
- The third line contains an integer: the search weight for the dates.
Input data will always be valid and will always be in the format described. There is no need to check.
Output Data
The result should be printed on the console as consecutive dates in "dd-mm-yyyy" format, sorted by date in ascending order. Each string must be in a separate line. If there are no existing magic dates, print "No".
Constraints
- The start and final years are integer numbers in the range [1900-2100].
- Magic weight is an integer in the range [1 … 1000].
- Allowed program time: 0.25 seconds.
- Allowed memory: 16 MB.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 2007 2007 144 |
17-03-2007 13-07-2007 31-07-2007 |
2003 2004 1500 |
No |
| Input | Output | Input | Output |
|---|---|---|---|
| 2012 2014 80 |
09-01-2013 17-01-2013 23-03-2013 11-07-2013 01-09-2013 10-09-2013 09-10-2013 17-10-2013 07-11-2013 24-11-2013 14-12-2013 23-11-2014 13-12-2014 31-12-2014 |
2011 2012 14 |
01-01-2011 10-01-2011 01-10-2011 10-10-2011 |
Hints and Guidelines
We start with the input data. In this case, we have 3 integers that should be read from the console, as this is the only entry and processing of input for the problem.
Having the start and end year, it is good to understand how we will go through each date, without being confused by how many days there are in the month and whether it is a leap year, and so on.
Loop Through Dates
For looping through the dates, we will take advantage of the functionality that gives us the LocalDate class, in Java. We will define a start date variable that we can do using the constructor that accepts a year, month, and day. We know the year is the starting year we read from the console, and the month and the day must be January and 1st respectively. In Java, the "constructor" of LocalDate accepts as the first argument the year, as second argument the month, and as the third argument the day of the month:

Once we have the start date, we want to create a loop that runs until we exceed the final year (or until we pass December 31 in the final year if we compare the full dates), increasing each day by one day.
To increase by one day in each rotation, we will use a method of LocalDate – plusDays(…), which will add one day to the current date. The method will take care instead of us whether to skip the next month, how many days there is a month, and everything around the leap years.
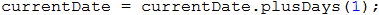
Caution: since the LocalDate.plusDays(…) method returns the "new" date, it is important to assign the result, not just to call the method!
Finally, our loop may look like this:
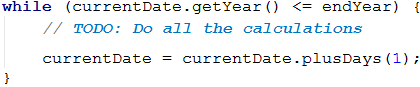
Note: we can achieve the same result with a for loop: the initialization of the date goes to the first part of for, the condition is preserved and the step is the increase by 1 day.
Calculating Date Weight
Each date consists of exactly 8 characters (digits) – 2 for the day (d1, d2), 2 for the month (d3, d4), and 4 for the year (d5 to d8). It means that we will always have the same calculation every time, and we can benefit from this to define the formula statically (i.e., not to use loops, referring to different numbers from the date, but write the whole formula). To be able to write it, we will need all digits from the date in individual variables to make all the necessary multiplications. Using the operations of division and remainder on the individual components of the date, using the getDayOfMonth(), getMonthValue(), and getYear() properties, we can retrieve each digit.
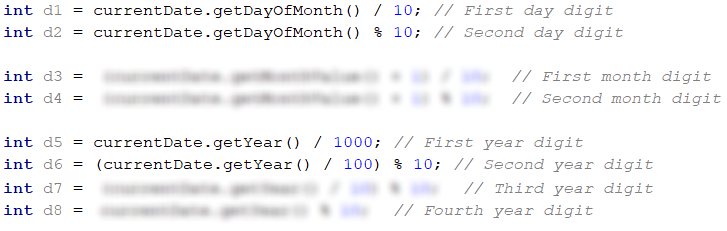
Let us also explain one of the more interesting lines here. Take, for example, the second digit of the year (d6). We divide the year by 100, and we take a remainder of 10. What do we do? First, we eliminate the last 2 digits of the year by dividing by 100 (Example: 2018/100 = 20). With the remainder of 10, we take the last digit of the resulting number (20 % 10 = 0) and so we get 0, which is the second digit of 2018.
What remains is to do the calculation that will give us the magical weight of a given date. In order not to write all multiplications as shown in the example, we will apply a grouping. What we need to do is multiply each digit with those that follow it. Instead of typing d1 * d2 + d1 * d3 + … + d1 * d8, we can shorten this expression to d1 * (d2 + d3 + … + d8) for grouping when we have multiplication and addition. Applying the same simplification for the other multiplications, we get the following formula:
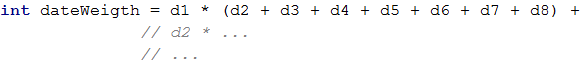
Printing The Result
Once we have the weight calculation of a given date, we need to check and see if it matches the magical weight, to know if it should be printed, or not. Checking can be done using a standard if block, taking care to print the date in the correct format. To format data as required in the problem, we will use DateTimeFormatter class.
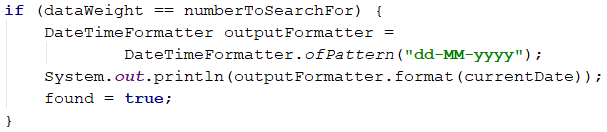
Caution: Since we iterate over the dates from initial to final, they will always be ordered in ascending order as it is in the requirements.
Finally, if we have not found an eligible date, we will have a false value in the found variable, and we will be able to print No.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/663#1.
Problem: Five Special Letters
Two numbers are given: start and end. Write a program that generates all combinations of 5 letters, each among the sets of {'a', 'b', 'c', 'd', 'e'} so that the weight of these 5 letters is a number in the range [start … end], inclusive. Print them in alphabetical order, in a single row, separated by a space.
The weight of the letters is calculated as follows:
weight('a') = 5;
weight('b') = -12;
weight('c') = 47;
weight('d') = 7;
weight('e') = -32;
The weight of the sequence of the letters c1, c2, …, cn is calculated by removing all the letters that are repeated (from right to left) and then calculating the formula:
weight(c1c2…cn) = 1 * weight(c1) + 2 * weight(c2) + … + n * weight(cn)
For example, the weight of bcddc is calculated as follows:
First, we remove the repeating letters and get bcd. Then we apply the formula: 1 * weight('b') + 2 * weight('c') + 3 * weight('d') = 1 * (-12) + 2 * 47 + 3 * 7 = 103.
Another example: weight("cadae") = weight("cade") = 1 * 47 + 2 * 5 + 3 * 7 + 4 * (-32) = -50.
Input Data
The input data is read from the console. It consists of two numbers:
- The number for our start.
- The number for our end.
Input data will always be valid and will always be in the format described. There is no need to check.
Output Data
The result should be printed on the console as a sequence of strings, sorted in alphabetical order. Each string must be separated from the next one by a single space. If the weight of any of the 5 letter strings does not exist within the specified range, print "No".
Constraints
- Numbers for start and end are integers in the range [-10000 … 10000].
- Allowed program time: 0.25 seconds.
- Allowed memory: 16 MB.
Sample Input and Output
| Input | Output | Comment |
|---|---|---|
| 40 42 |
bcead bdcea | weight("bcead") = 41 weight("bdcea") = 40 |
| Input | Output |
|---|---|
| -1 1 |
bcdea cebda eaaad eaada eaadd eaade eaaed eadaa eadad eadae eadda eaddd eadde eadea eaded eadee eaead eaeda eaedd eaede eaeed eeaad eeada eeadd eeade eeaed eeead |
| Input | Output |
|---|---|
| 200 300 |
baadc babdc badac badbc badca badcb badcc badcd baddc bbadc bbdac bdaac bdabc bdaca bdacb bdacc bdacd bdadc bdbac bddac beadc bedac eabdc ebadc ebdac edbac |
| Input | Output |
|---|---|
| 300 400 |
No |
Hints and Guidelines
Like every problem, we start the solution by reading and processing the input data. In this case, we have two integers that can be processed with a combination of the Integer.parseInt(…) and Scanner.nextLine() methods.

We have several main points in the problem – generating all combinations with a length of 5 including the 5 letters, removing repeating letters, and calculating weight for a simplified word. The answer will consist of every word whose weight is within the given range [firstNumber, secondNumber].
Generating All Combinations
To generate all combinations with a length of 1 using 5 symbols, we would use a loop from 0 to 4, as we want each number of the loop to match one character. To generate any combinations of length 2, using 5 characters (i.e. "aa", "ab", "ac", …, "ba", …), we would create two nested loops each running through the digits from 0 to 4, and we will once again make sure that each digit matches a specific character. We will repeat this step 5 times, so we will finally have 5 nested loops with indexes i1, i2, i3, i4, and i5.

Now that we have all 5-digit combinations, we must find a way to "turn" the five digits into a word with the letters from 'a' to 'e'. One of the ways to do that is to predefine a simple string that contains the letters that we have
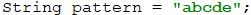
and for each digit, we take the letter from the particular position. This way, the number 00000 will become "aaaaa", and the number 02423 will become "acecd". We can create the 5-letter string in the following way.

Another way: we can convert the digits to letters by using their arrangement in the ASCII table. The expression 'a' + i return the result 'a' in case i = 0, 'b' in case i = 1, 'c' in case i = 2, etc.
This way we already have generated all 5-letter combinations and can proceed with the following part of the problem.
Attention: as we have chosen a pattern that takes into consideration the alphabetical arrangement of the letters, and cycles are run appropriately, the algorithm will generate the works in alphabetical order and there is no need for additional sorting before printing the output.
Removing Repetitive Letters
Once we have the finished string, we have to remove all the repeating symbols. We will do this by adding the letters from left to right in a new string, and each time before adding a letter, we will check if it already exists – if it does, we will skip it, and if it doesn't, we will add it. To begin with, we will add the first letter to the starting string.
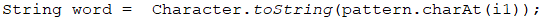
Then we will do the same with the other 4, checking each time with the following condition and the .indexOf(…) method. We can use a loop by fullWord (leaving it to the reader for exercise), and it can be done lazily by copy-paste.

The .indexOf(…) method returns the index of the particular element if it is found, or -1 if the item is not found. Therefore, every time we get -1, it means that we still do not have this letter in the new string with unique letters and we can add it, and if we get a value other than -1, this will mean we already have the letter, and we'll not add it.
Calculating Weight
Calculating the weight is simply going through the unique word (word) obtained in the last step, and for each letter, we need to take its weight and multiply it by the position. For each letter, we need to calculate what value we will multiply its position by, for example, by using a switch construction.

Once we have the value of that letter, we should multiply it by its position. Because the indexes in the string differ by 1 from the actual positions, i.e., index 0 is position 1, index 1 is position 2, etc., we will add 1 to the indexes.
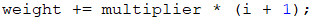
All intermediate results obtained must be added to the total amount for each letter of the 5-letter combination.
Preparing The Output
Whether a word needs to be printed is determined by its weight. We need a condition to determine if the current weight is in the range [start … end] passed to the input at the start of the program. If this is the case, we print the full word (fullWord).
Be careful not to print the word with unique letters. It was only needed to calculate the weight!
The words are separated with a space, and we will accumulate them in an intermediate variable result, which is defined as an empty string at the beginning.
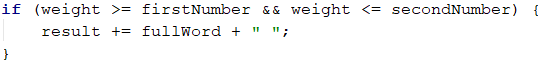
Final Touches
The condition is met unless we do not have a single word in the entered range. To find out, if we have found a word, we can check whether the string result has its initial value (i.e., an empty string). If it does, we print No else print the whole string without the last space (using the .trim ()) method.
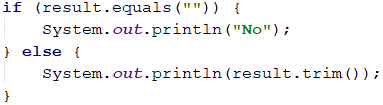
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/663#2.